
Particularly in C, where arrays are closely tied to pointer arithmetic, this makes for a simpler implementation: the subscript refers to an offset from the starting position of an array, so the first element has an offset of zero. In these three, sequence types (C arrays, Java arrays and lists, and Lisp lists and vectors) are indexed beginning with the zero subscript. This usage follows from design choices embedded in many influential programming languages, including C, Java, and Lisp. See also: Comparison of programming languages (array) § Array dimensions Dijkstra's criteria for preferring this convention are in detail that it represents empty sequences in a more natural way ( a ≤ i < a ?) than closed "intervals" ( a ≤ i ≤ ( a − 1) ?), and that with half-open "intervals" of naturals, the length of a sub-sequence equals the upper minus the lower bound ( a ≤ i < b gives ( b − a) possible values for i, with a, b, i all integers). Discussing possible designs of array ranges by enclosing them in a chained inequality, combining sharp and standard inequalities to four possibilities, demonstrating that to his conviction zero-based arrays are best represented by non-overlapping index ranges, which start at zero, alluding to open, half-open and closed intervals as with the real numbers. Dijkstra in his pertinent note Why numbering should start at zero argued that arrays subscripts should start at zero as the latter being the most natural number. The optimization was nevertheless important. BCPL was first compiled for the IBM 7094 the language introduced no run-time indirection lookups, so the indirection optimization provided by these arrays was done at compile time. Martin Richards, creator of the BCPL language (a precursor of C), designed arrays initiating at 0 as the natural position to start accessing the array contents in the language, since the value of a pointer p used as an address accesses the position p + 0 in memory. However, just as the first derivative precedes the second derivative, so also does the zeroth derivative (or the original function itself) precede the first derivative.Ĭomputer programming Origin Such usage corresponds to naming an element not properly belonging to the sequence but preceding it: the zeroth derivative is not really a derivative at all. In some mathematical contexts, zero-based numbering can be used without confusion, when ordinal forms have well established meaning with an obvious candidate to come before first for instance, a zeroth derivative of a function is the function itself, obtained by differentiating zero times.
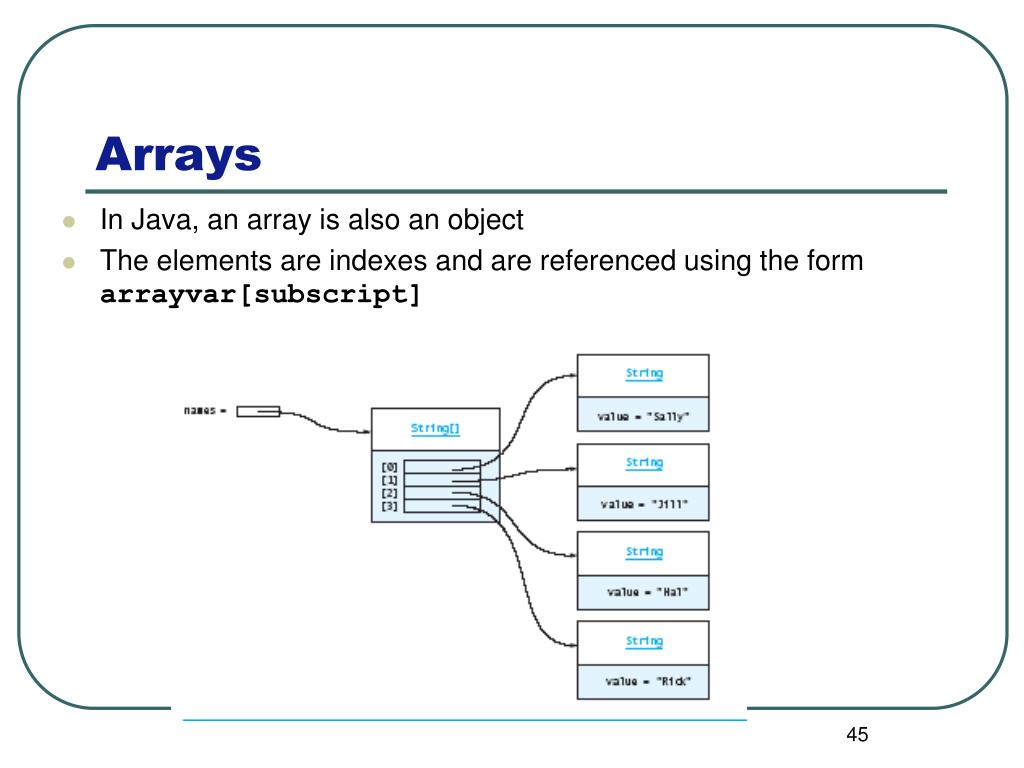
In computer science, array indices usually start at 0 in modern programming languages, so computer programmers might use zeroth in situations where others might use first, and so forth.

Numbering sequences starting at 0 is quite common in mathematics notation, in particular in combinatorics, though programming languages for mathematics usually index from 1. There is not wide agreement regarding the correctness of using zero as an ordinal (nor regarding the use of the term zeroth), as it creates ambiguity for all subsequent elements of the sequence when lacking context.
In some cases, an object or value that does not (originally) belong to a given sequence, but which could be naturally placed before its initial element, may be termed the zeroth element. Under zero-based numbering, the initial element is sometimes termed the zeroth element, rather than the first element zeroth is a coined ordinal number corresponding to the number zero. Zero-based numbering is a way of numbering in which the initial element of a sequence is assigned the index 0, rather than the index 1 as is typical in everyday non-mathematical or non-programming circumstances.


 0 kommentar(er)
0 kommentar(er)
